Rotational motion

Introduction

This lesson will extend the concepts learned in Lesson 3.1 to motion that is circular, i.e., motion of an object in a circular path about a specific point. There will be some new terminology which some students may already know the names but not the formal definitions.

Uniform Circular Motion

Key Concepts

The key concepts for this part of the lesson are:

Understand circular motion.
Calculate motion properties of a rotating body.

Lesson

Angular Velocity

If an object is traveling in a circle the path of the object is circular, not linear as shown in the figure below.
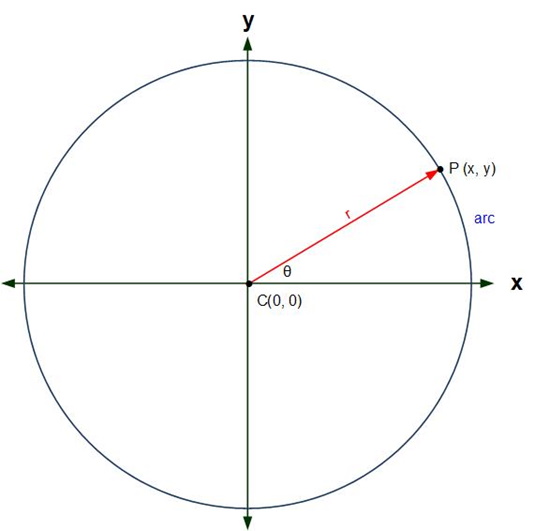
rotating-1

Examining this figure, the value of the radius has no effect on the change in angle. The formula for angular velocity is:

$\omega=\frac{\Delta{\theta}}{t}$

Angular Acceleration

If the rate of change of angle increases, or decreases, (i.e., ω changes), then there is acceleration. The formula for angular acceleration is:

$\alpha=\frac{\Delta{\omega}}{t}$

We can now use the knowledge from Linear Motion to get the following equations:

$\omega_f=\omega_i+\alpha{t}$

$\Delta{\theta}=\omega_it+\frac{1}{2}\alpha{t^2}$

Tangential Velocity

What about the physical velocity, i.e., the velocity felt at a point on a circle? In the figure, below, we see a possible scenario:
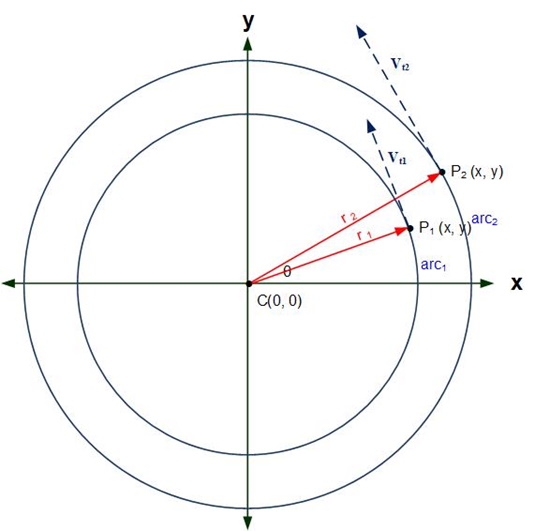
rotating-2

Here we see that arc₁ is smaller in length than arc₂, which should tell us that, physically, P₂ is travelling faster than P₁; it may not be obvious, but V_t1 has a smaller magnitude than V_t2. This physical speed is Tangential Velocity. The formula for this is:

$V_t=\frac{\Delta{arc}}{t}$

Doing some substitution, we can determine the relationship between angular velocity and tangential velocity:

$\Delta{\theta}=\frac{\Delta{arc}}{r}$

$V_t=\frac{\Delta{\theta}\cdot{r}}{t}=\omega{r}$

Thus, the greater the radius of rotation, the greater the tangential velocity.

Example

Given an object, rotating at a constant speed of 3600 RPM, and the radius of rotation is 10cm, calculate the tangential velocity of the object.

$\omega=\frac{3600}{60}=60rev/s$

$\frac{1rev}{s}=2\pi{rad/s}$

$\omega=120\pi{\frac{rad}{s}\approx{376.9911rad/s}$

$V_t=120\pi\times{0.1}\approx{37.6991m/s}$

Centripetal Acceleration

The formula for centripetal acceleration is derived from what we already know of linear and rotational motion:

$a=\frac{\Delta{V_t}}{t}=\omega^2r$

Example

Using the same example as above, calculate the centripetal acceleration of the object.

$a=(120\pi)^2\times{0.1}\approx{14212.2303m/s^2}$

$centripetal-math$

Centripetal Force

The most common effect of centripetal force is in a centrifuge. It is not always obvious, but centripetal force is towards the center of rotation (centripetal means center seeking).

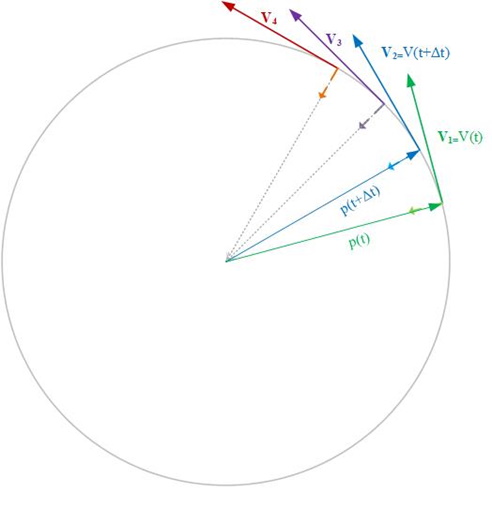
rotating-3

This figure shows that the motion felt, tangential velocity, is always perpendicular to the radius of rotation. Yet, for the object to rotate, and not fly off into space, there needs to be some entity that keeps the rotation in a circular path. This is Centripetal Force. (There will be more on forces in the next lesson, but, for now, just think that some force must exist to make this all work.)

The formula for Centripetal Force is:

$F_c=\frac{mV_{t}^2}{r}$

Example

Calculate the centripetal force on the object, using the rotation as per the previous examples, if its mass is 25 g.

$F_c=\frac{0.025\times{(37.6991)^2}}{0.1}\approx{355.3055N}$

$centripetal-force-math$

Exercises & Assignments

Complete the Rotational Motion worksheet. Once complete proceed to Moodle to complete Knowledge Check 11 - Rotational Motion (strongly recommended to be completed prior to attempting Lab 3).

Rotational motion

Introduction

Uniform Circular Motion

Key Concepts

Lesson

Angular Velocity

Angular Acceleration

Tangential Velocity

Example

Centripetal Acceleration

Example

Centripetal Force

Example

Exercises & Assignments

Outcome Home

PHYS1521 Home