Linear Mechanics

Introduction

This lesson will extend the concepts learned in Lesson 3.1 to include how to get object moving and what happens when they are moving. To accomplish use this introduction of Newton’s Laws.

Modern mechanics has evolved from the classical mechanics of Sir Isaac Newton; the inclusion of the work by Albert Einstein, and others, has changed, somewhat, the work done by Sir Isaac Newton. The fundamentals of Newton’s work are summarized in his three laws.

Newton’s First Law
Every body persists in a state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed.

Newton’s Second Law
The acceleration of a body is proportional to (and in the same direction as) the net external force acting on the body, and inversely proportional to the mass of the body:
$F=mA$

Newton’s Third Law
To every action there is always an equal and opposite reaction. Or, the force of two bodies on each other are always equal and directed in opposite directions.

So, looking at the 1^st law why does an object not keep moving, it eventually comes to a stop, after it is compelled to move? Friction. Friction is an external force that opposes motion, but it was quite the statement in its day. Also, a force is required to move an object.

The 2^nd law’s formula is so simple but very important; it is fundamental to this lesson. Using the standard units for mass and acceleration we get:

$1N=1kg\times{1\frac{m}{s^2}}=1kg\frac{m}{s^2}$

It is important that a force does not produce velocity, only acceleration; an application of the linear motion equations from lesson 3.1 will yield a given velocity, and displacement, over a period.

Finally, the 3^rd law. This law will come into play in almost every situation. For example, a body that is seen to be not moving does not mean that there are no forces acting on it, simply that this could be true, or all the forces balance each other out in opposite directions and thus no motion.

One thing that is important in real world physics is that the continued application of an applied force, over a very large period, does not result in speeds greater than the speed of light. Additionally, as Einstein formulated, and what has been learned so far, everything is relative to a certain view of the world, game world or real world.

Simple Forces

Key Concepts

The key concepts for this part of the lesson are:

Calculation of net force
Calculation of acceleration on a body

Lesson

As an application of the 1^st and 3^rd laws consider an object sitting at rest on a table, or other suitable platform. What is known about this object? It has mass, and therefore weight (please note that mass and weight are different). All force values must be vectors; examining the 2^nd law it should be obvious that this is a vector multiplied by a scalar, which results in a vector.

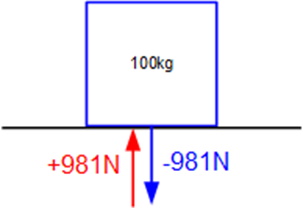
forces-01

The value of -981N is the result of the 1^st law:
$Weight=mass\times{Gravity}$

The other value, 981N, balances out weight, $-981+981=0$ . What is this force? This is the equal and opposite force of gravity (3^rd law) called Normal Force (F_N); F_N is a reactive force in that it is the surface pushing back, assuming it does not bend or break, and will increase and decrease depending on the weight of the object resting on the surface.

Consider the scenario shown in the figure below in which an external force is applied to the object.
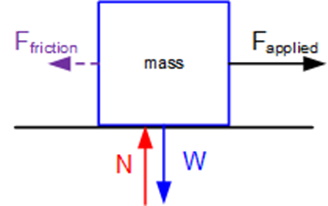
forces-02

In this scenario what would have to exist for the block to move? The applied force must overcome friction. How can the amount, magnitude, of friction be determined? The value of friction depends on the surfaces involved and whether the object is initially at rest or initially moving. It is important here to make mention that Friction, like Normal Force, is a reactive force, and will increase to a maximum value before the object will be able to move.

The two types of Friction are static (the object is not moving) and kinetic (the object is already in motion). The notations will be F_s and F_k respectively, and are calculated as:

$F_s=\mu_sF_N$ and $F_k=\mu_kF_N$

Refer to an internet source, for some standard values of μ.

As an example, using the scenario shown in the figure above, with $F_{applied}=250N$ and $\mu_s=0.2$ calculate F_net:

$F_s=(0.2)(981)=196.2N$

The direction of this vector must be opposite the relative motion of the surfaces, or $F_s=-196.2N$ . Next calculate the net force. To do this correctly all external forces must be used and used as vectors.

$F_{net}=W+F_N+F_s+F_{applied}=\left[\begin{array}{c}0\\-981\end{array}\right]+\left[\begin{array}{c}0\\981\end{array}\right]+\left[\begin{array}{c}-196.2\\0\end{array}\right]+\left[\begin{array}{c}250\\0\end{array}\right]=\left[\begin{array}{c}53.8\\0\end{array}\right]N$

Questions:

Why do friction and applied force have no y-component?
What if the applied force was only 150N?
What is the acceleration on this object? $A=\frac{F_{net}}{m}=\frac{1}{100}\left[\begin{array}{c}53.8\\0\end{array}\right]=\left[\begin{array}{c}0.538\\0\end{array}\right]m/s^2$

Consider the scenario shown in the figure below, where the applied force is at an angle.
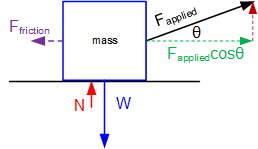
forces-06

Given F_applied=250N@30^o:

$F_{applied}=\left[\begin{array}{c}F_{applied}cos\theta\\F_{applied}sin\theta\end{array}\right]=\left[\begin{array}{c}250cos(30)\\250sin(30)\end{array}\right]\approx{\left[\begin{array}{c}216.5064\\125.0000\end{array}\right]N}$

As there is a vertical component to the applied force, F_N is now calculated as:

$F_N=-W+F_{applied}sin\theta=-981+125=856N$

Now calculate the max friction as:

$F_s=\mu{F_N}=-(0.2)(856)=-171.2N$

Finally, calculate the net applied force:

$F_{net}=W+F_N+F_s+F_{applied}=\left[\begin{array}{c}0\\-981\end{array}\right]+\left[\begin{array}{c}0\\856\end{array}\right]+\left[\begin{array}{c}0\\-171.2\end{array}\right]+\left[\begin{array}{c}216.5064\\125.0000\end{array}\right]=\left[\begin{array}{c}45.3064\\0\end{array}\right]N$

Questions:

Why is net force reduced?
What is the acceleration on the object?

$A=\frac{F_{net}}{m}=\frac{1}{100}\left[\begin{array}{c}45.3064\\0\end{array}\right]=\left[\begin{array}{c}0.4531\\0\end{array}\right]m/s^2$

Consider the scenario shown in the figure below, where the object is at rest on an inclined surface.
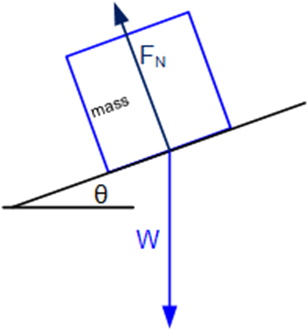
forces-03

Note that weight is always perpendicular to the ground, not the surface the object is resting on, and Normal Force is always perpendicular to the surface the object is resting on. As the surface, not the ground, is responsible for providing F_N. The weight vector needs to be split into its components, relative to the surface, not the ground as shown in the figure below.
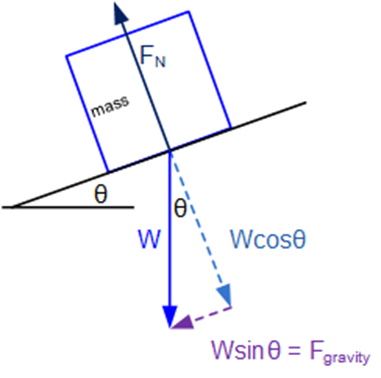
forces-04

Note: It can be proven that the angle θ of the incline is the same angle of the right triangle formed by the components of weight.

Question now is whether the object is moving or not. In this initial state which direction is friction? It will be up the ramp regardless of the whether the object is moving or not. Using the same object, and friction coefficient as before, but now have the ramp angle at 10^o calculate net force. First calculate weight.

$Wsin\theta=(100)(-981)(sin(10))\approx{-170.3498N}$

$Wcos\theta=(100)(-981)(cos(10))\approx{-966.0964N}$

Next calculate $\Vert{F_N}\Vert$ :

$\Vert{F_N}\Vert=-Wcos(10)\approx{966.0964N}$

Next the maximum friction:

$\Vert{F_s}\Vert=(0.2)(966.0964)\approx{193.2993N}$

Determine if the object is moving. It is clear that $\vert{-170.3489}\vert{<\vert{193.2193}\vert}$ therefore the object is at rest; the x-component of gravity was not sufficient to overcome friction, therefore $F_{net}=0N$ . What would happen if the incline angle were increased to 20^o?

$Wsin\theta=(100)(-981)(sin(20))\approx{-335.5218N}$

$Wcos\theta=(100)(-981)(cos(20))\approx{-921.8385N}$

$\Vert{F_N}\Vert=-Wcos(20)\approx{921.8385N}$

$\Vert{F_s}\Vert=(0.2)(921.8385)\approx{184.3677N}$

At this point it should be clear that the x-component of weight exceeds, in magnitude, the maximum value of friction, therefore the object will be moving down the ramp:

$\Vert{F_{net}}\Vert=-336.5218+0+184.3677\approx{-151.1541N}$

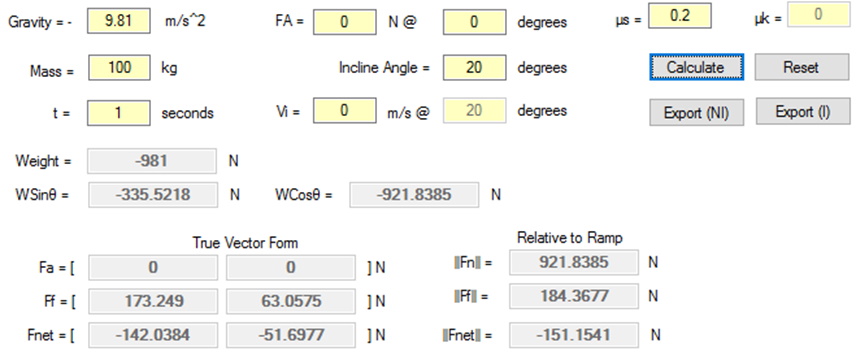
$forces-math-1$

Questions:

Does this answer seem reasonable?
What about the True Vector Form values in the screenshot?
Could an applied force be calculated to prevent the object from moving down the ramp?
Could an applied force be calculated to move the object up the ramp?
What is the acceleration of the object down the ramp?

$\Vert{A}\Vert=\left(\frac{1}{100}\right)(-151.1541)\approx{-1.5115m/s^2}$

$forces-math-2$

The *True Vector Form values are not relative to the incline, but relative to the ground.

Another scenario would be:
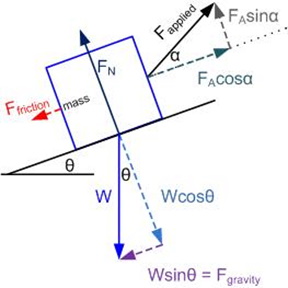
forces-05

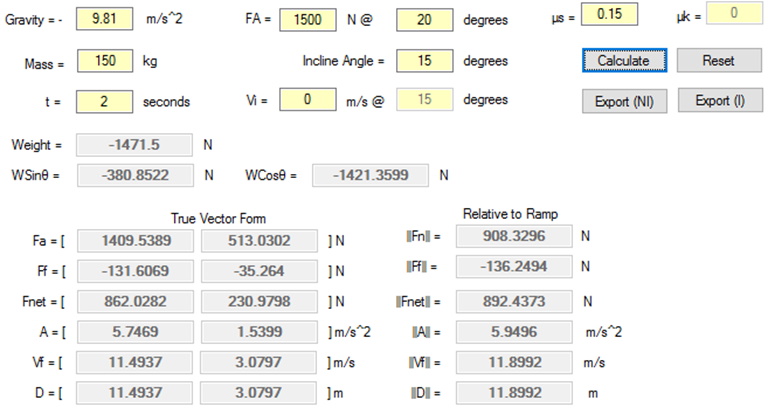
How would you solve this type of scenario?
$forces-math-3$

forces-note

Exercises & Assignments Complete the Linear Mechanics worksheet. Once completed, proceed to Moodle to complete Knowledge Check 12 - Linear Mechanics (strongly recommended to be completed prior to attempting Lab 3).

Linear Mechanics

Introduction

Simple Forces

Key Concepts

Lesson

Outcome Home

PHYS1521 Home